We list some open problems regarding the Strahler-Horton number on random trees \(T_n\).

The definition

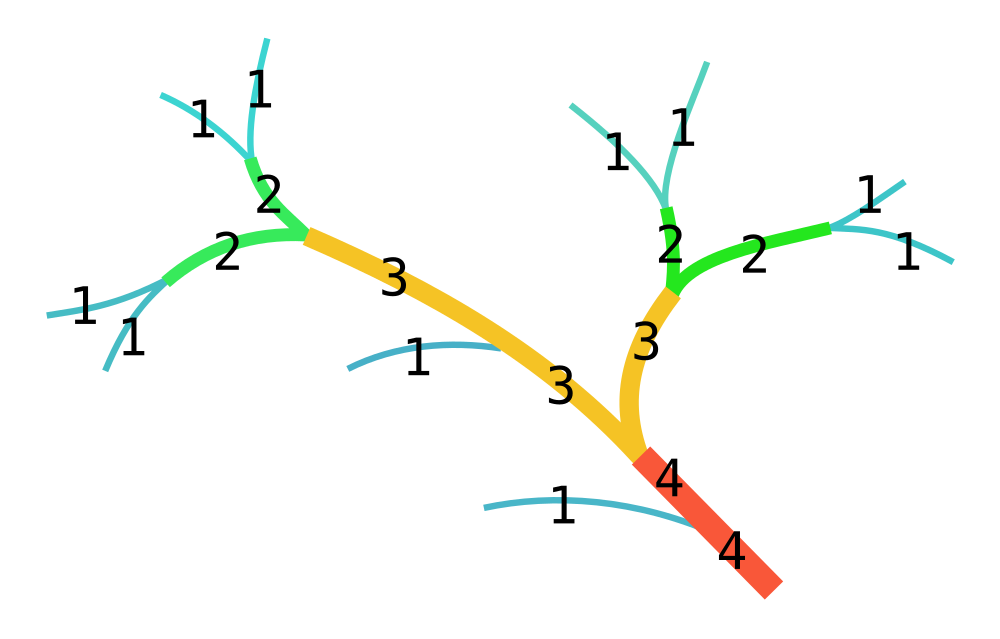
One may assign a Strahler number to all nodes of a tree, in bottom-up order, as follows:

• If the node is a leaf (has no children), its Strahler number is one.

• If the node has one child with Strahler number i, and all other children have Strahler numbers less than i, then the Strahler number of the node is i again.

• If the node has two or more children with Strahler number i, and no children with greater number, then the Strahler number of the node is \(i + 1\).

Horton-Strahler number is a relatively popular topic. See recent papers here.

What is known

Conditional Galton-Watson trees

Uniform binary tree

Luc Devroye and Kruszewski (1995) has shown that for a uniform random binary tree of \(n\) nodes, its Horton-Strahler number \(S_n\) satisfies \[\mathbb{E}\left(S_n\right)=\log_4(n)+O(1), \qquad \mathbb{P}\left(\left| S_n-\log_4(n)\right| \geq x\right)\leq \frac{D}{4^x}\] for some constant \(D>0\).

The \(O(1)\) term has been studied in great details by Flajolet (Prodinger 2012) using generating function.

t-ary trees

Drmota and Prodinger (2006) studied the Horton-Strahler number of uniform random trees \(T_n\) with degrees in a finite set.

They definition of Strahler-Horton Number is slightly different. Let \(c_1\geq c_2\geq \text{...}\geq c_t\) be the Horton number of subtrees of node u, then Horton number of the subtree u is defined by \[S(u)=\max \left(c_1,c_2+1,\ldots ,c_t+t-1\right)\] (When \(t\leq 2\), this reduces to original Horton number definition). Their result shows that the Horton number of \(S_n=S(T)\) has that \[\mathbb{E}\left(S_n\right)=\log_4(n)+O(1), \qquad \mathbb{P}\left(\left| S_n-\log_4(n)\right| \geq x\right)\leq O\left(2^{-y}\right)\] uniformly for \(0\leq y\leq \left(\frac{1}{2}-\epsilon \right) \log_4(n)\). This somewhat surprising result basically says that \(S_n\) is always \(\log_4(n)\) regardless of the offspring distribution. The proof uses generating functions.

Split trees (Binary Search Trees)

L. Devroye and Kruszewski (1996) showed that for binary tries, i.e., binary split trees with split vector \(\left(V_1,1-V_1\right)\) and \(V_1\) has Bernoulli \(p\) distribution, we have \[\frac{S_n}{\log (n)}\overset{p}{\to }\frac{1}{\log \left(\frac{1}{\min (p,1-p)}\right)}\] The proof uses and upper bound called Balance number and a lower bound called Fill level, which converges to the same limit in this case.

For binary search trees, the upper bound Balance number is used to show that \[\frac{S_n}{n \log }\leq \frac{1}{\log (3)}\] with high probability (Kruszewski 1999). This is conjectured as the right scale. Though the lower bound given by Fill level is far away from the upper bound.

What’s more can be done?

• Can we get a probabilistic proof for the universal \(\log_4(n)\) for Galton-Watson trees?

• Can we find the lower bound for the binary search trees?

• Can there be a general result on split trees?

• What is the Horton Number for RRT or Preferential Attachment?

References