The sum of n uniform [0,1] random variables - You don't need to prove this

Update: Svante Janson told me yesterday that the integral I had at the end of this post is known as the beta integral, see 5.14.1 of NIST Handbook of Mathematical Functions, 2019 ed.

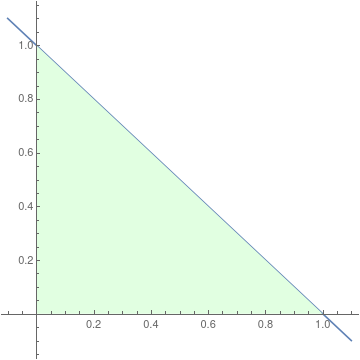
What is the size of the green triangle in the following picture? Of course it is $1/2$. Everybody knows.

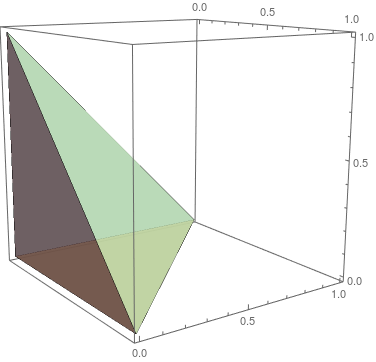$Two dimensional polyhedron $S_2$$ What about this polyhedron? $Three dimensional polyhedron $S_3$$ If you still remember a bit Euclidean geometry, then you will see this is $\frac{1}{6}=\frac{1}{2}\frac{1}{3}$. Do you see where I am going?

Let's define an $n$-dimension polyhedron

$$ S_n = \{(x_1,\dots,x_n) \in \mathbb R^n:1>x_1>0,\dots, 1>x_n>0, 1>x_1+\dots+x_n\}. $$

Then the previous two pictures are just $S_2$ and $S_3$. If you compute the volume of $S_n$, you will see

$$ \mathrm{vol}(S_n)= \int_{(x_1,\dots,x_n) \in S_n} \mathrm{d}(x_1,\dots,x_n) =\frac{1}{n!} . $$

There is another way to view this. Let $U_1,\dots,U_n$ be $n$ independent uniform random variables on $[0,1]$, what is the probability that $U_1+U_2 \dots U_n \le 1$? It is precise the volume of $S_n$ and is thus $1/n!$.

Can we get this without doing the integral? Yes. We have

$$ \mathbb P\{U_1+U_2 \dots U_n \le 1\} = \mathbb P\{U_1+U_2 \dots U_{n-1} \le 1-U_n\} = \mathbb P\{U_1+U_2 \dots U_{n-1} \le U_n'\} $$

where $U_n'$ is again an independent uniform $[0,1]$ random variable. For the event $U_1+U_2 \dots U_{n-1} \le U_n'$ to happen, we need that $U_n'$ is the maximum one among the $n$ variables, which has probability $1/n$. Conditioning on this, $U_1,\dots,U_{n-1}$ are independent and uniformly distributed on $[1,U_n']$. So the conditional probably of $U_1+U_2 \dots U_{n-1} \le U_n'$ is $1/(n-1)!$ by induction. Put it together, we have

$$ \mathbb P\{U_1+U_2 \dots U_n \le 1\} = \mathbb P\{U_1+U_2 \dots U_{n-1} \le U_n'|\text{$U_n'$ is the maximum}\} \mathbb P\{\text{$U_n'$ is the maximum}\} = \frac{1}{n!}. $$

Why do I bring up this? A few days ago, I found the following identity

$$ \int_{(x_1,\dots,x_n) \in S_n} (x_1 \dots x_n)^{-1/k} \mathrm{d}(x_1,\dots,x_n) = \Gamma\left(\frac{k-1}{k}\right)^n \Gamma(1+n-n/k)^{-1} , \qquad k \ge 2. $$

Let $k \to \infty$, then we get back our $1/n!$. Does this have a probabilistic explanation? I do not know. Maybe you know?