Consider a random multi-graph process \(G_{m}(t)\) constructed with the following procedure. Let \(G_{m}(1)\) be just a single vertex \(1\). Given \(G_{m}(t)\), we construct \(G_{m}(t+1)\) by adding a vertex \(t+1\) and connect it to \(m\) vertices chosen independently and uniformly at random for vertices \(1, \cdots, t\). This can be a multi-graph since there maybe more than one edges between two vertices. But there can be no self-loops and the graph is always connected.
I came up with this model while reading about P2P network. These are computer networks that collaborate in a decentralized way to share resource. The most well-known examples include BitTorrent and Bitcoin. When a computer join such a network, it chooses a random a few number of other computers (neighbours) to connect to. How neighbours are chosen exactly differs from network to network. But in general, there is no particular preferences to any one in the network. (This is contra to social networks, where the most well-connected are more likely to be connected to others.)
I did some simulation on this model and found something rarely intriguing -- the diameter of the model seems to concentrates very quickly to two consecutive integers. See the picture below. The number above each plot is the number of nodes \(t\). The histogram shows the distribution of the diameters of 2000 samples for each \(t\).
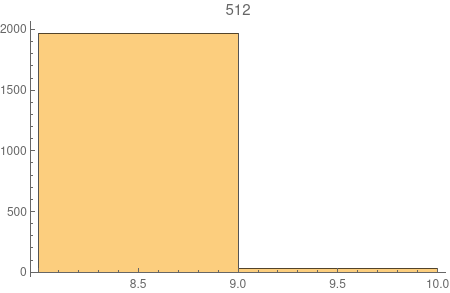
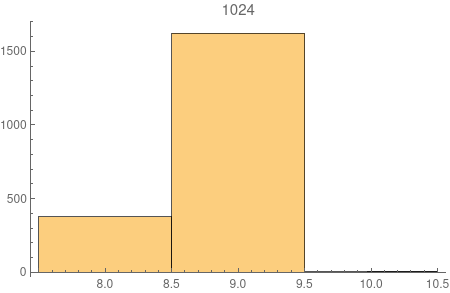
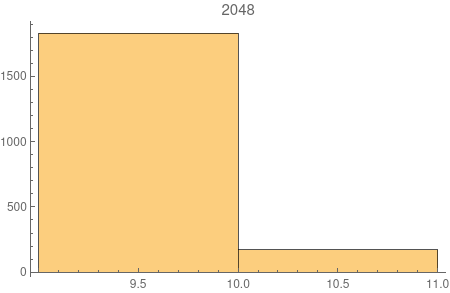
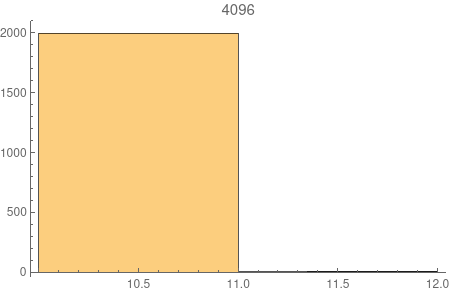
It's not difficult to show the diameter is of the order \(\log n\) following along the line of this paper. But can we actually prove the two-point concentration?